If all you care about is The Bathroom Remodel, skip this post

The Doktah called me at work the other day and left me a message with an example of a limit where “plugging in infinity” didn’t work. At first, I thought she was right, and I wasn’t going to blog about it because it would mean I was wrong, and it’s my blog, so I don’t have to admit to being wrong if I don’t want to. But it bugged me all day, so I looked it up in my Calculus book when I got home that night.

I’m still right.

Her example:






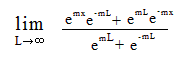
Now, if you plug in infinity for L, you get






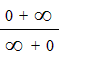
This appears to reduce to ∞/∞ = 1.

But! One thing that I admit to sort of forgetting because I don’t actually take limits anymore is that ∞/∞ is undefined. So while you can cancel ∞²/∞ to get ∞, you can’t cancel ∞/∞ to get 1. You have to use L’Hopital’s rule*. But back in the day when I used to take limits on a regular basis, this never bothered me or made me get any wrong answers in my problem sets because I knew the rule. Anytime you get an undefined solution like ∞/∞ or ∞/0 (or anything over 0, for that matter), you have to take another step to solve the problem.

So, nyah nyah.

*L’Hopital’s rule just says that the limit of the derivatives of each term in the function is the same as the limit of the function, so you just take limit of the derivatives of the separate terms until you get something that is defined. I put this explanation in a footnote because I would bet that 90% of my readers didn’t even read to the end of this entry because it is full of equations. I can’t really blame them.